西工大新闻网9月2日电（许勇）近日，计算数学与计算物理领域著名期刊《Journal of Computational Physics》在线报道了西北工业大学理学院数学系非线性随机动力学团队许勇教授在非高斯列维噪声激励下系统动力学方程研究方面成果。该研究成果以“Path integral solutions of the governing equation of SDEs excited by Lévy white noise”为题在此期刊394期发表。

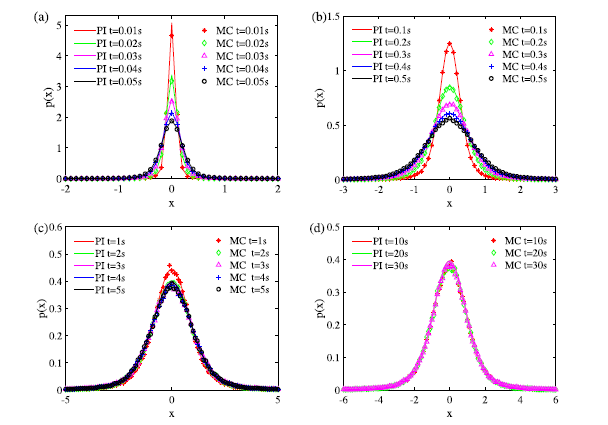
不同时刻下系统解的概率密度函数

随机现象在自然界中广泛存在，列维噪声激励下的随机系统为这些随机现象提供了通用的数学描述。针对列维噪声激励下的随机系统虽然已经开展多年的研究，现有研究成果主要集中在列维噪声的激励下随机系统的解的定性描述。而对于此类系统的解所满足的概率分布的定量描述始终是一个难题。这是因为对于列维噪声激励下的随机系统，其解的概率密度函数所满足的控制方程（即福克普朗克方程）本质上为分数阶偏微分方程，它是一个非局部（nonlocal）的偏微分方程，只有在极少数特殊参数下可以得到其解析解，并且用于求解此类方程的数值方法有限。因此，有关此类方程的求解始终是相关领域的研究难题和关注焦点。

针对这一难题，许勇教授团队通过发展路径积分法，提出此类分数阶偏微分方程的路径积分求解方法。首先，从列维噪声激励下的随机系统对应的福克普朗克方程出发，推导了路径积分所需的短时解，并从特征函数的角度验证了该短时解的正确性。进而根据短时解给出了该方程的路径积分求解过程。最后借助所发展的方法，对不同的外部函数、稳定性参数情形进行计算，验证了路径积分法求解分数阶福克普朗克方程的有效性。通过对比所得路径积分结果与已有方法的结果，可以发现许勇教授团队所提出的路径积分法具有更高的计算精度及效率。

《Journal of Computational Physics》为中科院分区1区top期刊，为计算数学与计算力学领域国际三大顶级期刊之一。它关注物理问题中的计算方法，鼓励在应用数学、物理、力学、统计学、应用几何等跨学科领域有关先进的数学和数值建模方面做出原始的科学贡献。

全文链接：https://www.sciencedirect.com/science/article/pii/S0021999119303547

（审稿：王洲航）